Act4.5 - Force de gravitation
Retour sur le cours⚓︎
La force de gravitation est une grandeur qui dépend de la masse des objets qui s'attirent et de la distance entre ces deux objets. Elle se calcule avec la relation :
Les masses sont données en kg et la distance en m. \(G\) est la constante de gravitation qui n'est pas à confondre avec g l'intensité de la pesanteur.
\(G\) est une constante qui sera toujours donnée dans les exercices et elle vaut : \(G=6,67 \times 10^{-11} N \times m^2 / kg^2\).
Voici le lien d'une animation qui vous permettra de vous entraîner à faire des calculs sur l'utilisation de cette formule.
Correction des entraînements⚓︎
Ex1. Force de gravitation entre la Terre et la Lune⚓︎
La Lune n'est pas à une distance constante de la Terre. Cette distance varie entre 356000km et 406000km. Lors d'une expérience, on observe une distance Terre-Lune \(d = 3,64 × 10^8 m\).
- Calculer la valeur de la force de gravitation exercée par la Terre sur la Lune.
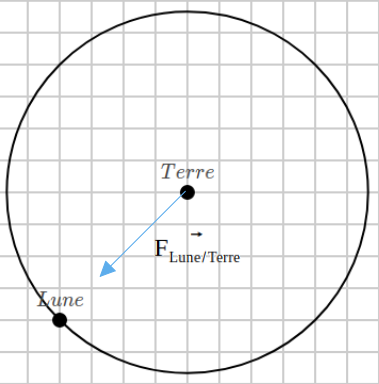
- Sur le schéma ci-contre, ajouter la force de gravitation exercée par la Lune sur la Terre (on la notera \(\vec F_{Lune/Terre}\)) avec pour échelle : 1 cm pour \(1 × 10^{20} N\).
- On utilise la formule : \(F_{Lune/Terre}=G \times {{m_{Lune} \times m_{Terre} \over d^2}}\).
On pense à convertir la distance pour qu'elle soit en mètre : \(d = 3,64 \times 10^8m\). Soit le calcul :
La force exercée par la Lune sur la Terre a pour valeur \(2,20 \times 10^{20}N\).
- Pour mettre à l'échelle, on peut passer par la proportionnalité :
| Valeur de la force (N) | Longueur du vecteur (cm) | |
|---|---|---|
| Échelle | \(1 × 10^{20}\) | \(1\) |
| Force | \(2,2 × 10^{20}\) | \(2,2\) |
Le vecteur partira du centre de la Terre, et sera dirigé vers la Lune. Il mesurera 2,2 cm.
Ex2. Force de gravitation entre un lion et un éléphant⚓︎
Un lion de masse \(m_1 = 153 kg\) et un éléphant de masse \(m_2 = 5,5 tonnes\) se situent à une distance \(d = 91m\) l'un de l'autre.
- Calculer la valeur de la force gravitationnelle entre les deux corps.
- Calculer la valeur de la force gravitationnelle exercée par la Terre sur l'éléphant.
- Calculer la valeur du poids de l'éléphant.
- Comparer les deux valeurs et conclure.
1. On utilise la formule \(F_{éléphant/lion}=G \times {{m_{1} \times m_{2} \over d^2}}\).
On convertit la masse en kg \(m_2=5,5 \times 1000 kg\). Soit le calcul :
2. En appliquant un raisonnement similaire, on obtient :
3. On utilise la formule : \(P_{éléphant} = m_{éléphant} \times g = 5,5 \times 1000 \times 9,81 \approx 54 000 N\).
4. Les deux valeurs sont très proches. On peut donc conclure que le poids et la force de gravitation sont en fait deux actions identiques à la surface de la Terre, mais avec des mises en applications différents.
Ex3. Masse d'un globule rouge⚓︎
Calculer la masse d'un globule rouge dont le poids sur Terre est 0,40 pN (Aide : \(1pN = 10^{-12}N\)).
On transforme la formule \(P=m\times g\) en \(m={P \over g}\).
On a donc après calcul : \(m = {0,4\times 10^{-12} \over 9,81}=4,0\times 10^{-13} kg\). Soit une masse extrèmement faible.
Ex4. En route vers le Soleil ?⚓︎
- Le Soleil exercice-t-il une force gravitationnelle sur vous ?
- Déterminer la force de gravitation exercée par le Soleil sur un élève qui pèse 50 kg.
- Déterminer la force de gravitation exercée par la Terre sur ce même élève.
- Pourquoi ne nous envolons-nous pas vers le Soleil ?
1. Oui le Soleil exerce une force de gravitation sur nous. Mais elle doit être très faible.
2. Sachant la distance correspondant à celle entre la Terre et le Soleil soit \(d=150000000000m=1,5\times 10^{11}m\). On peut écrire la formule :
3. On a vu à l'exercice 2 que le poids et la force de gravitation avait la même valeur sur la Terre. On peut donc écrire \(P_{élève}=F_{Terre/élève}=m_{élève}\times g\).
Ce qui donne : \(P_{élève}=F_{Terre/élève}=50\times 9,81 \approx 490N\).
4. On remarque que l'attraction de la Terre est beaucoup plus importante que celle du Soleil. On reste donc naturellement sur Terre.